A Scale balanced loss for bounding box regression
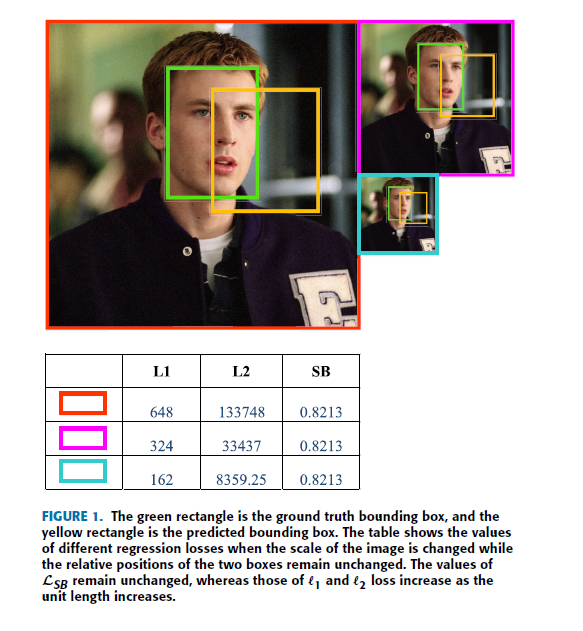
Abstract—Object detectors typically use bounding box regressors to improve the accuracy of object localization. Currently, the two types of bounding box regression loss are n-norm-based and intersection over union (IoU)-based. However, we found that these two types of losses have their drawbacks. First, forn-norm-based loss, large-scale objects are more likely to obtain a larger penalty than the smaller ones when calculating localization errors, which will cause regression loss imbalance. Second, n-norm-based loss has symmetry so that when the predicted bounding boxes are in some unique symmetrical relationships (i.e., Symmetric Trap), the regression loss remains unchanged. Third, for IoU-based loss, the overlap area and the union area do not change as the shape or relative position of two bounding boxes changes in some cases(i.e., Area Maze). To address these problems, we propose the scale balanced loss(LSB), which is asymmetric, position-sensitive, and scale-invariant. First, in order to obtain the property of scale invariance, it is designed as a fraction to eliminate the scale information contained in the numerator and denominator. Second, by incorporating the Euclidean distance between different corner points instead of the area, LSB is sensitive to the changes of coordinates of any corner point, so as to solve the area maze problem. Finally, by incorporating the diagonals of the overlap and the smallest enclosing rectangle, this fraction is no longer symmetric, thus solving the symmetry trap problem. To validate the proposed algorithm, we have replaced then-norm-based loss of YOLOv3 and SSD with LGIoU and LSB and evaluate their performance on Pascal Visual Object Classes and Microsoft Common Objects in Context benchmarks. The final results show that LSB has improved their average precisions at different IoU thresholds and scales. We envision that this regression loss can also improve the performance of other visual tasks.