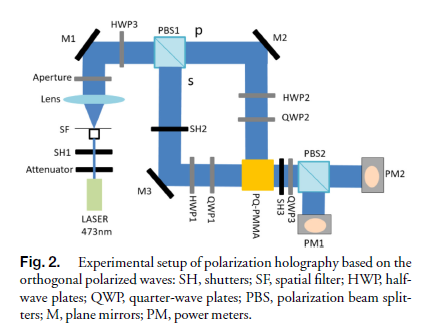
Investigation of the null reconstruction effect of an orthogonal elliptical polarization hologram at a large recording angle
Abstract—We report on the null reconstruction effect (NRE) of an elliptical polarization volume hologram with orthogonal elliptically, circularly, and linearly polarized waves, respectively. The NRE is a special phenomenon in polarization holography, which means the diffraction efficiency declines to zero when the hologram is reconstructed by an orthogonally polarized reading wave. In our previous work [Opt. Express24, 1641 (2016)OPEXFF1094-408710.1364/OE.24.001641; Opt. Lett.42, 1377 (2017)OPLEDP0146-959210.1364/OL.42.001377; Opt. Express23, 8880 (2015)OPEXFF1094-408710.1364/OE.23.008880], the NRE of polarization holography recorded by linear and circular polarization waves has been investigated. Compared with linear and circular polarization holography, elliptical polarization holography represents a more general and unified recording hologram. However, no work on the NRE of elliptical polarization holography, as far as we know, has been reported until now. In this paper, the NRE of elliptical polarization holography is investigated and demonstrated theoretically and experimentally. First, the conditions of achieving NRE in elliptical polarization holography are studied based on vector holography theory. The results indicate that the NRE is a common phenomenon in polarization holography written by linear, circular, and elliptical polarization waves. Then, a series of experiments of NRE in a polarization hologram written by orthogonal elliptically, circularly, and linearly polarized waves is carried out. The NRE of elliptical polarization holography is experimentally observed, and the results are in nice agreement with the theoretical analysis. The NRE of elliptical polarization holography is expected to be applied in high-density optical data storage and polarization-controlled holographic elements.